instalacja wideo (animacja cyfrowa) , 2012
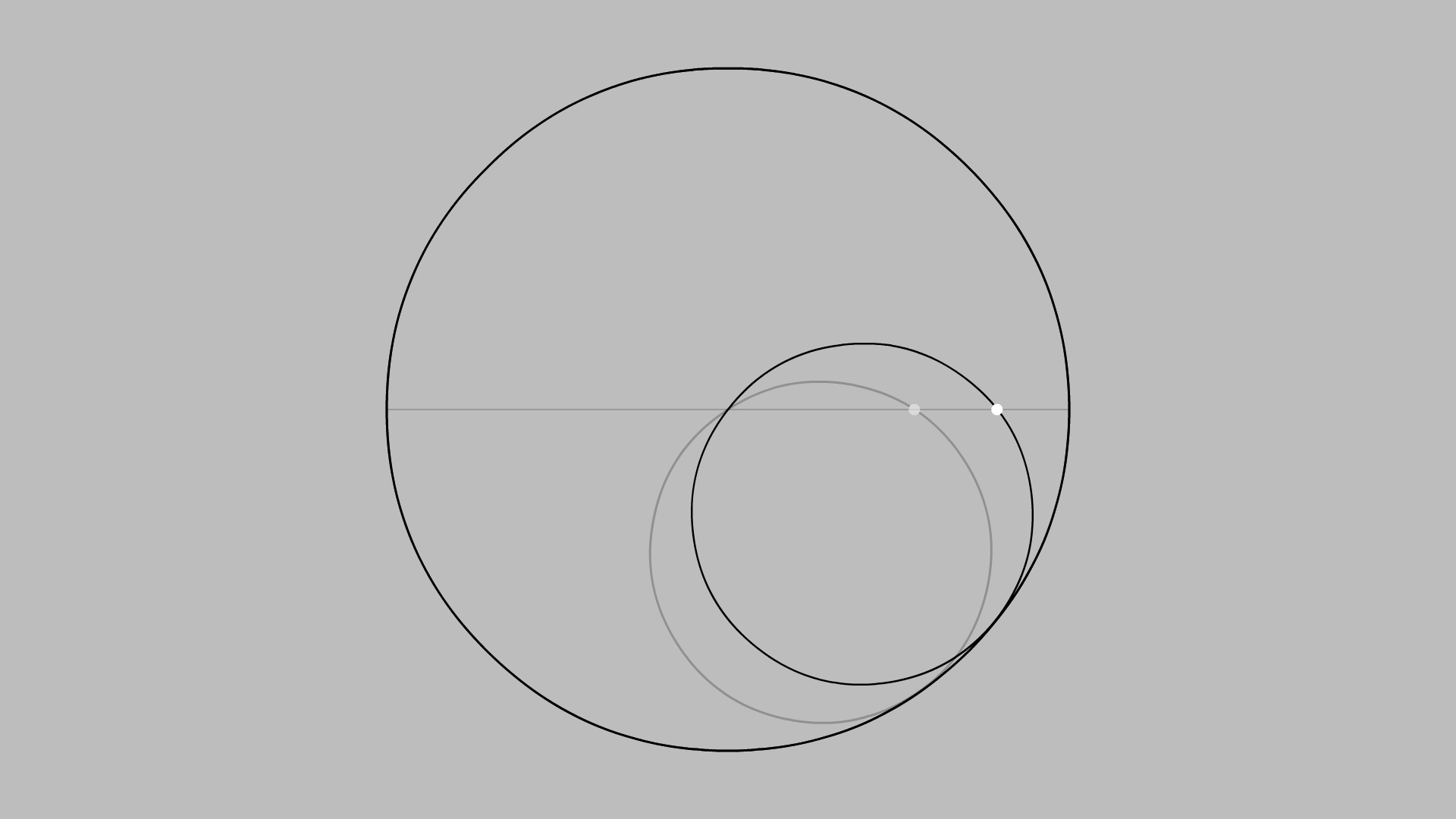
Widoczny na ekranie punkt porusza się z nawrotami wzdłuż odcinka. Animacja ujawnia prawdziwą naturę tego ruchu. Okazuje się, iż punkt leży na obwodzie koła, które toczy się wewnątrz koła o dwukrotnie większej średnicy. Zachodzi tu zatem bezpośrednie przełożenie ruchu okrężnego na ruch prostoliniowy, które zdaje się przeczyć naszym potocznym intuicjom.
Krzywa rysowana przez punkt leżący na obwodzie koła, które toczy się bez poślizgu wewnątrz koła większego to hipocykloida. Może ona przyjmować różne kształty, ale tylko w tym jednym wypadku,
kiedy to koło wewnętrzne ma dwukrotnie krótszą średnicę od koła zewnętrznego, hipocykloida redukuje
się do odcinka – średnicy zewnętrznego koła.
Analiza tego szczególnego przypadku hipocykloidy pomogła Galileuszowi znaleźć błędy w opisie ruchu dokonanym przez Arystotelesa i w konsekwencji zrozumieć istotę tego zjawiska. Fizyka arystotelesowska orzekała, że każda faza ruchu musi trwać jakiś czas, a każda zmiana ruchu wymaga fazy pośredniej
(tzw. quies media). Galileusz zauważył, że w wypadku hipocykloidy punkt zmienia kierunek swojego ruchu
w jednej, nierozciągłej w czasie chwili, bowiem ruch punktu po odcinku jest nierozerwalnie związany
z jednostajnym ruchem koła, w którym nic się przecież nie zmienia (nie ma żadnych wyróżnionych stanów). Spekulacje geometryczne stały się więc istotnym krokiem (punktem zwrotnym) na drodze do nowożytnej fizyki, która już wkrótce miała uzyskać swą ostateczną postać w pracach Izaaka Newtona.
Praca prezentowana na wystawach:
- Cudowne miejsce, Galeria Instytutu Polskiego w Bratysławie, Słowacja, październik 2012;
- In-motion, Hotel andel’s, Łódź, październik-listopad 2015;
- InMotion – wystawa sztuki kinetycznej, Politechnika Wrocławska, kwiecień 2016.
Opartą na tej samej koncepcji realizację interaktywną znaleźć można tutaj.